Der Goldene Schnitt
Der Begriff «Goldener Schnitt» bezeichnet die Teilung einer Strecke in zwei ungleich lange Teile, von denen sich der kleinere zum grösseren verhält wie der grössere zur Summe der Teile, d. h. zur ganzen Strecke.
Bezeichnet werden die Teile mit:
m = Minor (der Kleinere) und M = Major (der Grössere)
Als Proportion dargestellt: m:M = M : (m+M)
Als mathematische Gleichung dargestellt: x2 ± mx = m2
Man spricht, je nach Vorzeichen, von der inneren bzw. der äusseren stetigen Teilung.
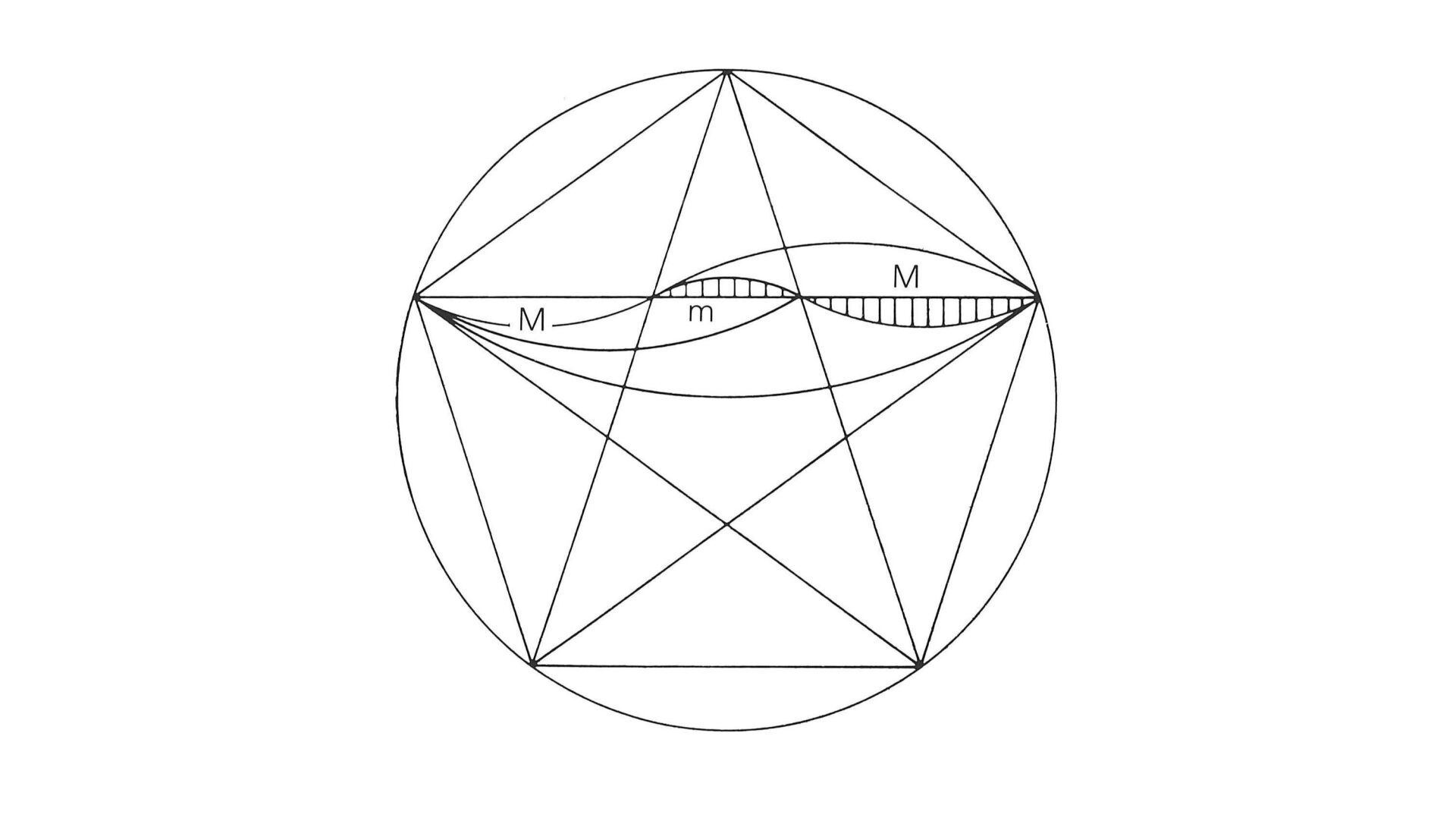
Der Name «Goldener Schnitt» stammt mutmasslich erst aus dem 19. Jahrhundert. Antike und Mittelalter kannten jedenfalls den «Goldenen Schnitt» unter dieser heute gebräuchlichen Bezeichnung nicht. Die stetige Teilung einer gegebenen Strecke im Goldenen Schnitt wurde um ca. 300 v. Chr. erstmals durchgeführt. Eine wesentliche Rolle spielte bei diesen Bemühungen das Pentagramm (Sternfünfeck), dessen Seiten sich stetig im Goldenen Schnitt teilen. Es liegt nicht mit absoluter Sicherheit fest, wem und zu welchem Zeitpunkt die exakte Konstruktion der Fünfeckteilung zuerst gelang. Vermutet wird lediglich, dass der pythagoreische Bund sich gründlich mit der Fünfeckskonstruktion befasst hatte.
Charakteristik
Charakteristik des Goldenen Schnittes zur Proportionierung vorgegebener Strecken
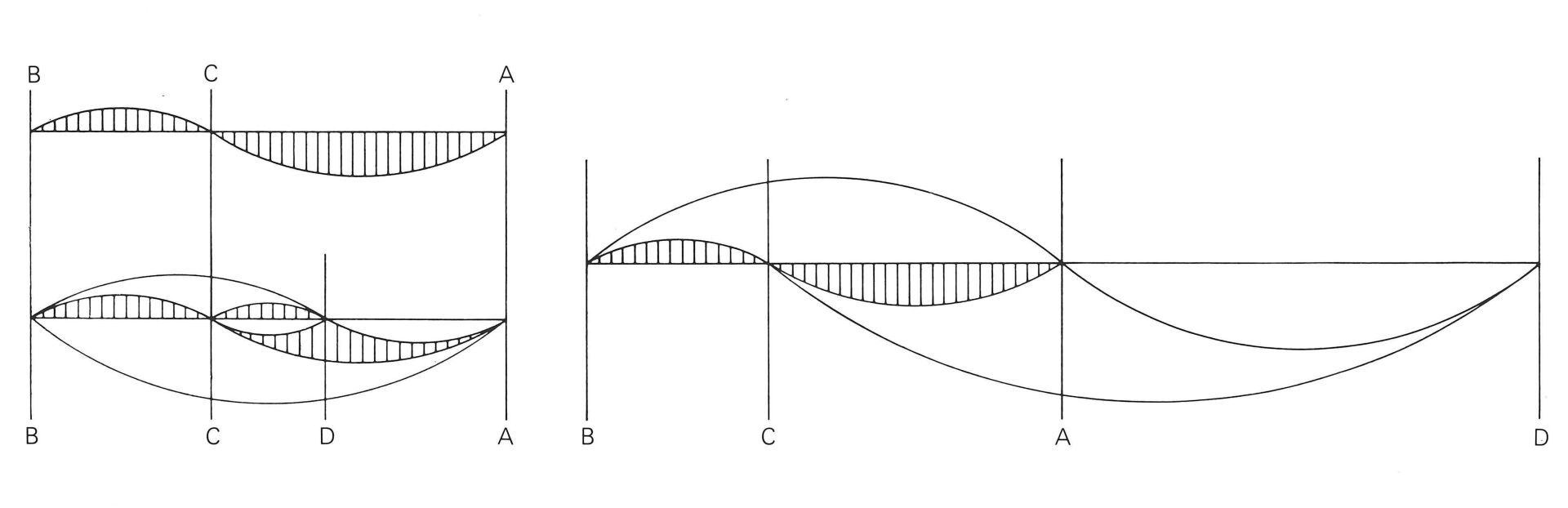
Eine Strecke AB wird in C durch den Goldenen Schnitt geteilt. Die Strecke lässt sich weiter unterteilen durch Abtragen der Länge CB von A bis D.
Resultat: AD : DB = DB : AB
Das bedeutet, dass jede Strecke zwei harmonische Teilungspunkte hat, deren Abstand DC abermals im Goldenen-Schnitt-Verhältnis steht zu AD und CB.
Die «Goldene Reihe»
Die gegebene Strecke AB wird in C golden geteilt. Wird die ursprüngliche Strecke AB über A hinaus verdoppelt, bilden die entstandenen drei Strecken eine «Goldene Reihe», deren Vergrösserung als auch die Verkleinerung stetig, d. h. bis ins Unendliche, fortgesetzt werden kann. Alle so ermittelten Strecken weisen immer das Verhältnis des Goldenen Schnittes auf. Dieses Teilungsprinzip wird z. B. in Le Corbusiers «Modulor» angewandt.
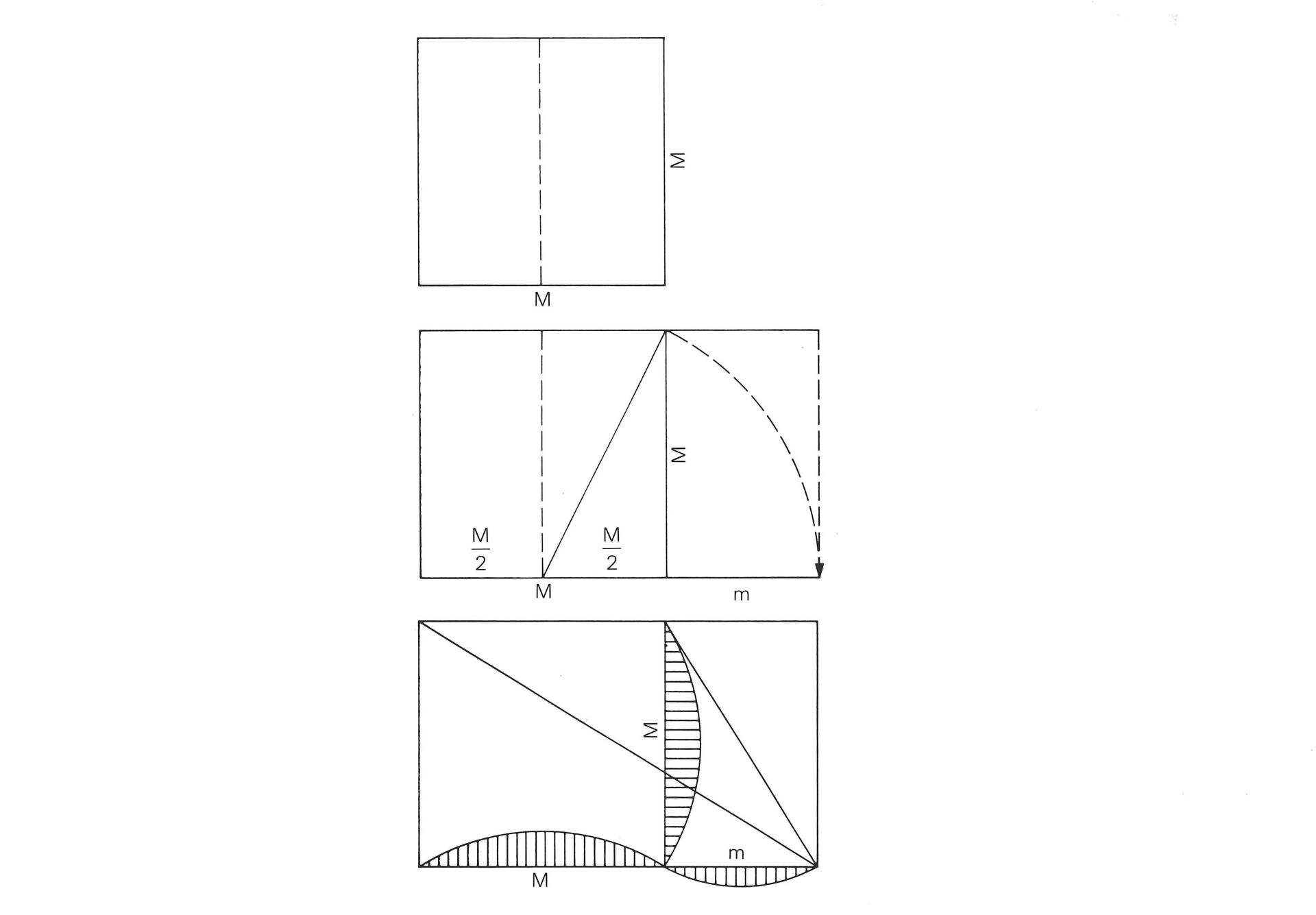
Charakteristik des Goldenen Schnittes zur Proportionierung von (Rechtecks-) Flächen
Durch Schwenken der Halbdiagonale eines lnitialquadrates entstehtein Rechteck, dessen Seitenverhältnisse dem Prinzip des Goldenenschnittes entsprechen.
Anwendung
Geometrische Konstruktion
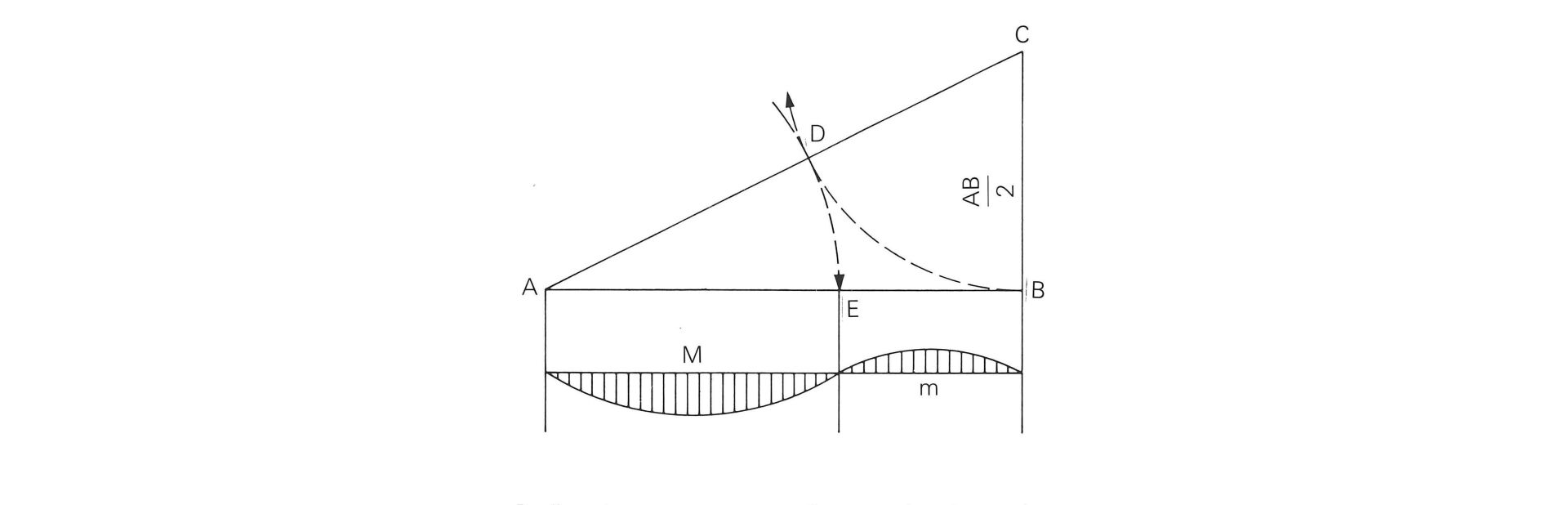
Gebräuchliche Konstruktionsmethode zur Goldenen Teilung einergegebenen Strecke AB:
- 1.
AB/2 senkrecht auf Punkt B der Strecke AB abtragen ergibt Punkt C.
- 2.
Punkte A und C verbinden
- 3.
Kreisbogen r = AB/ 2 um C schlagen ergibt Punkt D auf der Strecke AC.
- 4.
Kreisbogen r = AD um A schlagen ergibt Punkt E auf der Strecke AB. Punkt E teilt Strecke AB im Goldenen Schnitt.
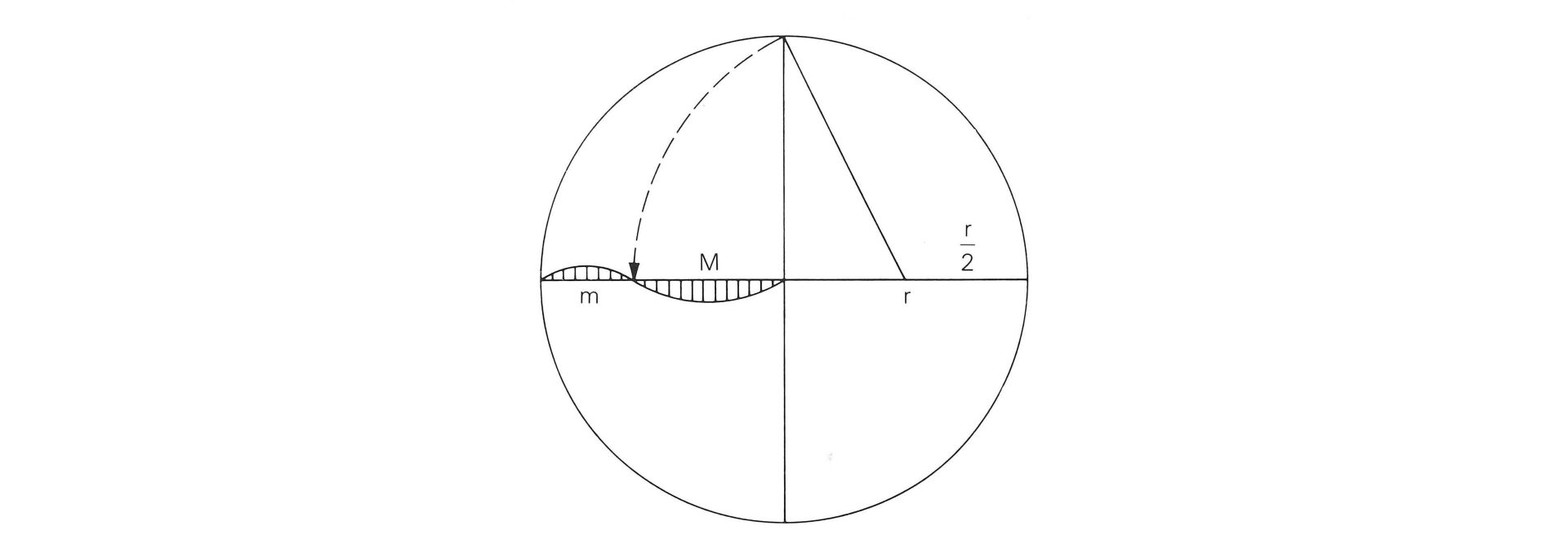
Konstruktion des Goldenen Schnittes auf dem Radius einesgegebenen Kreises:
Algebraische Ermittlung
ln die allgemeine Gleichung der stetigen Teilung wird für m = 1 eingesetzt:
x2 ± mx = m2
m = 1
Die Verhältniszahl des Goldenen Schnittes ergibt somit:
x2 + x = 1
x = –½ + √¼ + 1
x = –½ (1 – √5)
was für x einen Wert von x = 0,61803... ergibt.
Eigenschaft dieses Bruches:
1/0,61803... = 1,61803...
Das Verhältnis 1 : 0,61803... entspricht der Vergrösserung des Goldenen Schnittes.
Beispiele von Verhältniszahlen der «Goldenen Teilung»
Dokumentation
Schematische Darstellung der Hauptproportionen an der Stirnfassade des Parthenon
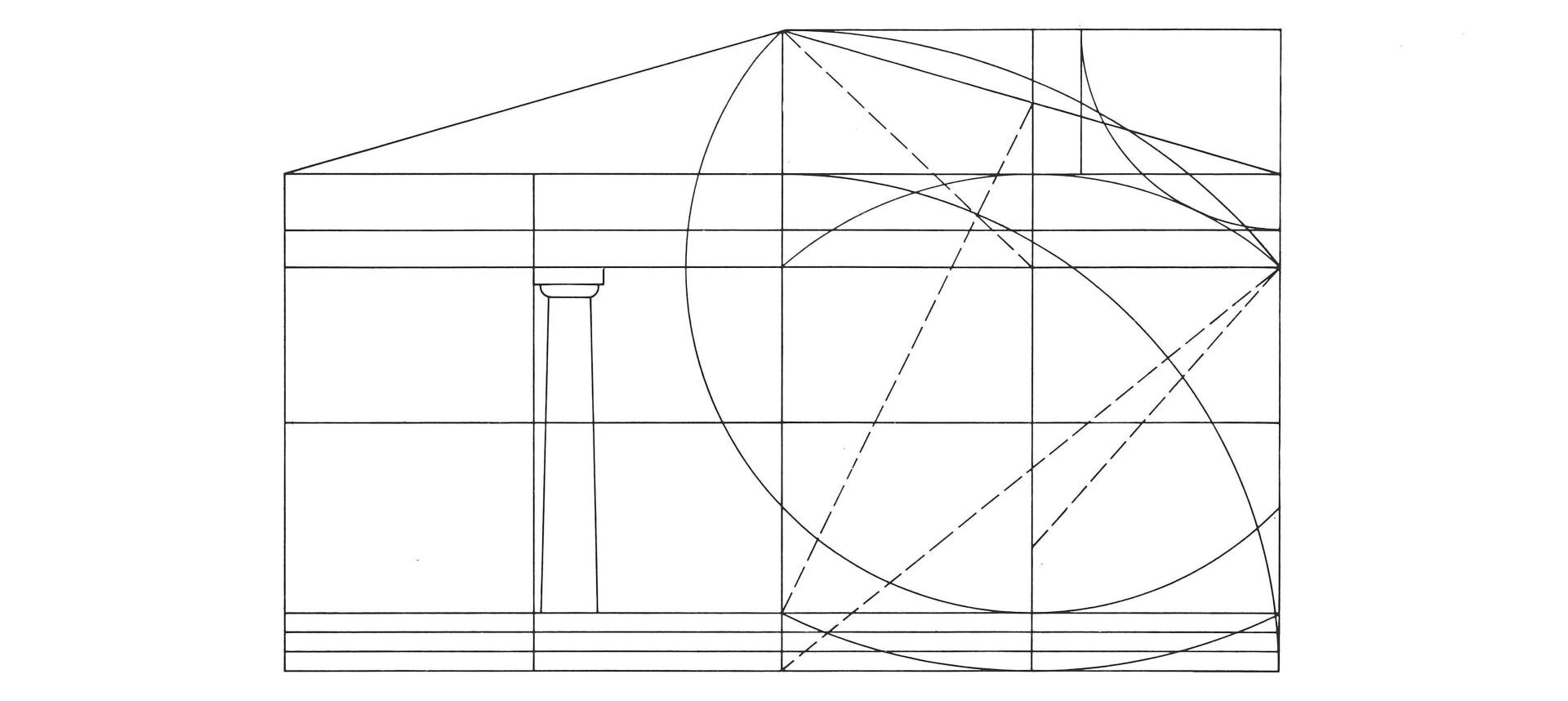
Stirnfassade des Parthenon
Darstellung des sogenannten «Goldenen Zirkels», einer Konstruktionshilfe für die Goldene Teilung
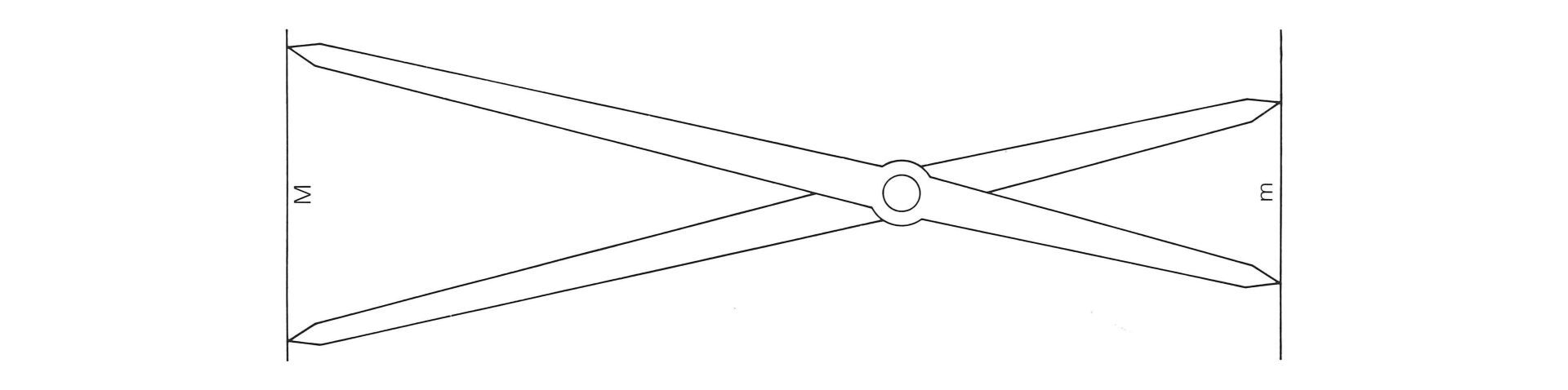
Goldener Zirkel
Schematische Darstellung zum Nachweis der Goldenen-Schnitt-Proportionen in der Natur
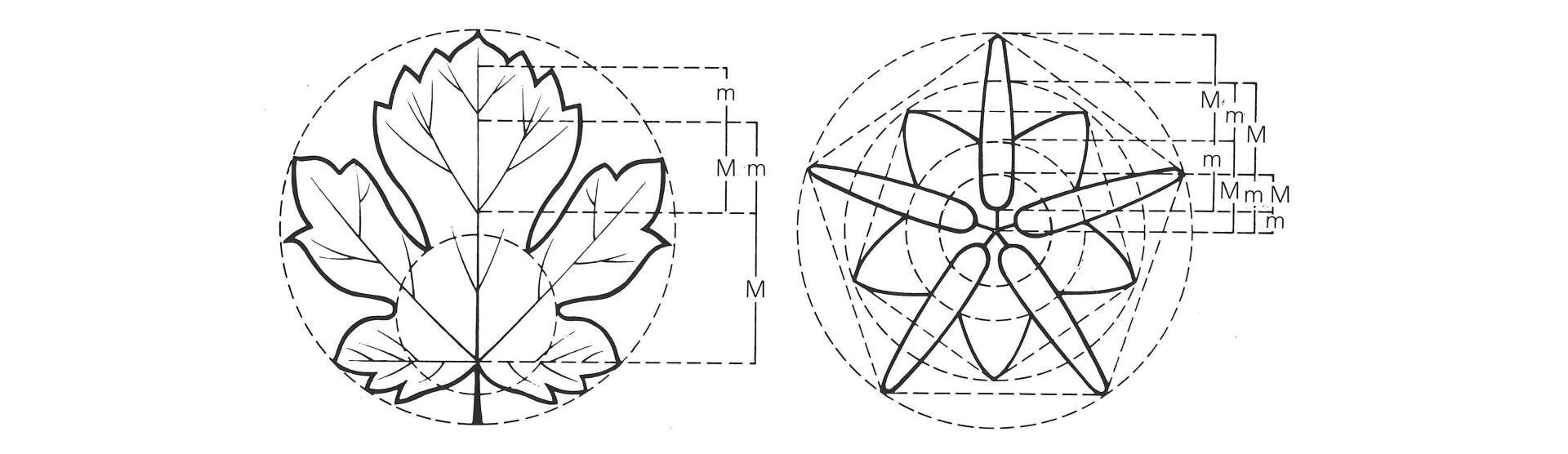
Goldenen-Schnitt-Proportionen in der Natur
Quellennachweis
Quellenangabe der Abbildungen sowie der übrigen verwendeten Unterlagen zu dieser Publikation:
– Bruno Munari, «Discovery of the Square»
– Otto Hagenmeier, «Der Goldene Schnitt», Ernst-Moos-Verlag, Heidelberg 1963
– Ernst Neufert, «Bauordnungslehre», Bauverlag GmbH. Wiesbaden-Berlin 1965