Le nombre d'or
L'expression «nombre d'or» désigne la proportion harmonique continue résultant de l'égalité de 2 rapports, soit respectivement rapport de 2 segments de droite et rapport du plus grand segment relativement à la somme des 2 segments.
Ces 2 segments portent les désignations:
m = mineur (le plus petit) et M = majeur (le plus grand)
La formule s'énonce: m : M = M : (m + M)
L'équation mathématique: x2 ± mx = m2
Selon le signe, on obtient une proportion constante intérieure (sous-traction), respectivement extérieure (addition).
L'expression «nombre d'or» ne fit son apparition dans le langage parlé qu'au XlXe siècle, l'antiquité et le moyen âge ne connaissant en tout cas pas le nombre d'or sous sa désignation actuelle.
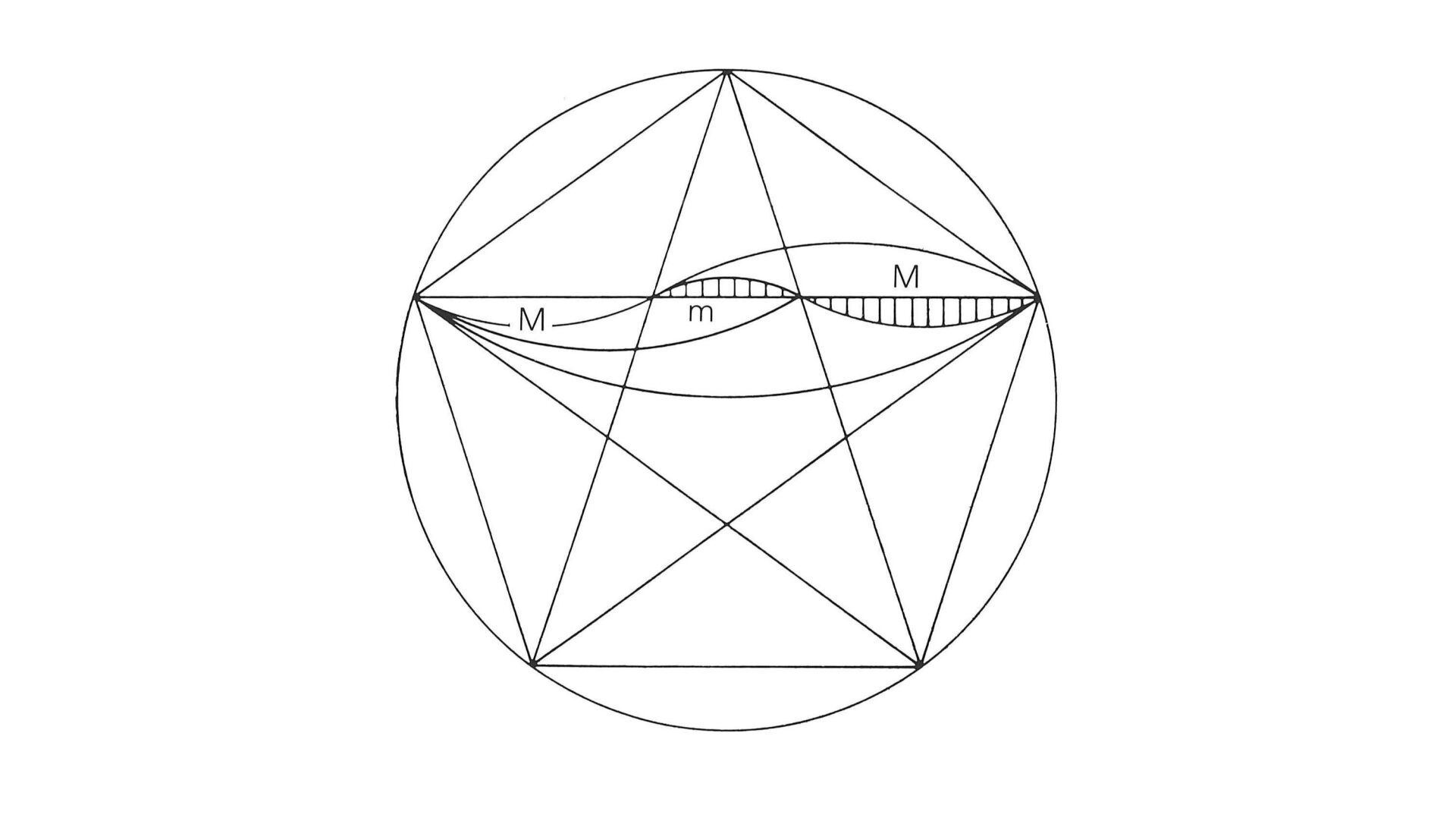
Les proportions harmoniques constantes d'une droite donnée relativement au nombre d'or ont été calculées pour la première fois aux environs de l'an 3OO av. J.-C. Le Pentagramme ou pentagone étoilé (étoile à 5 branches) joua un rôle considérable dans ce calcul, car ses côtés se divisent constamment selon le nombre d'or. A l'heure actuelle, il est impossible de dire avec certitude qui, et à quelle date, a fait, pour la première fois, la construction exacte de la division pentagonale. On pense toutefois que l'école de Pythagore aurait réalisé la première construction du pentagone.
Caractéristiques
Caractéristique du nombre d'or pour le proportionnement de segments donnés
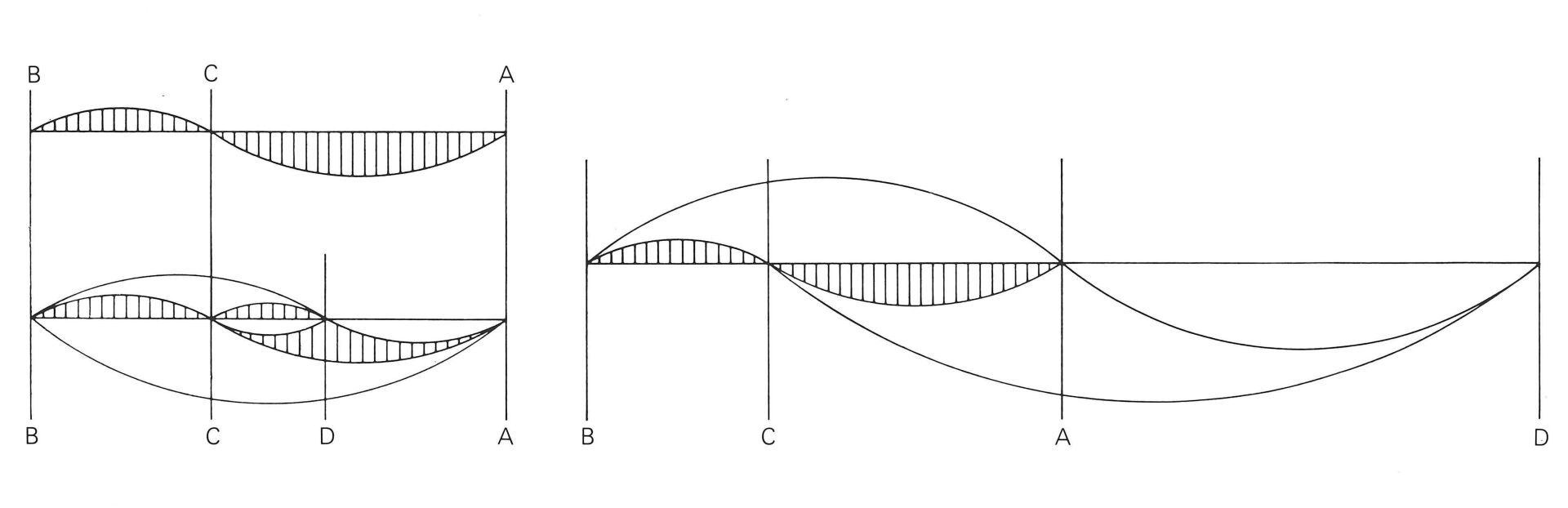
Soit un segment de droite AB coupé en C selon le nombre d'or. Si à partir du point A, nous reportons le segment CB, nous obtenons un point D et:
Résultat: AD : DB = DB : AB
Cela signifie que chaque segment a deux points harmoniques et que, selon le nombre d'or, le segment résultant DC est en proportion harmonique avec le segment AD d'une part et avec le segment CB d'autrepart.
La «série d'or»
Soit le même segment AB coupé en C selon le nombre d'or. En reportant à partir de A et sur le prolongement de la droite définie par les points A et B un segment AD égal au segment AB, on obtient 3 segments qui forment une «série d'or». On peut tracer, selon le même principe, et ce jusqu'à l'infini, d'autres segments dans le sens positif (agrandissement) ou négatif (réduction) tout en conservant la proportion du nombre d'or. Ce principe de proportionnement est utilisé, par exemple, dans le «Modulor» de Le Corbusier.
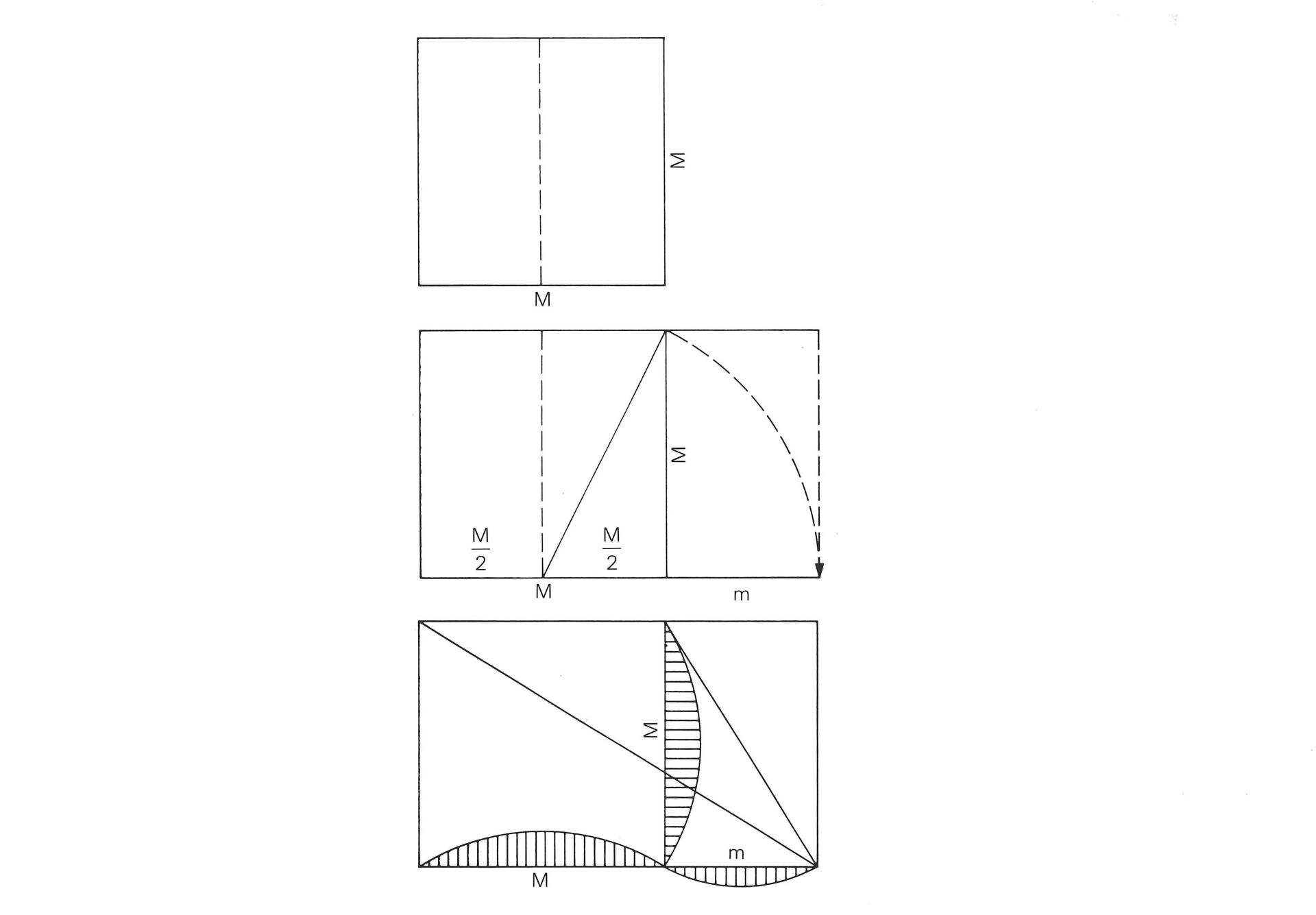
Caractéristique du nombre d'or pour le proportionnement de surfaces rectangulaires
Soit la demi-diagonale d'un carré; par rabattement de cette demi-diagonale sur la base du carré initial, on obtient un rectangle dont le rapport des côtés correspond au principe du nombre d'or.
Application
Construction géométrique
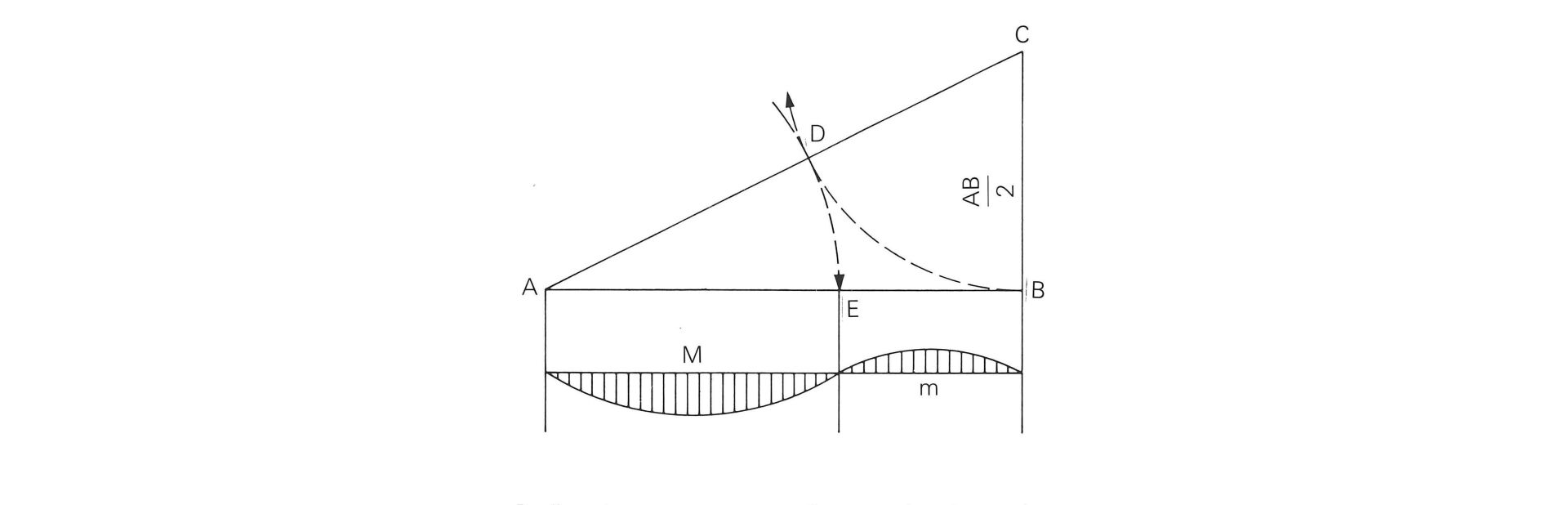
Méthode de construction usuelle de proportionnement d'un segmentde droite AB donné selon le nombre d'or:
- 1.
Elever en B une perpendiculaire à la droite AB et y reporter le segment AB/2; on obtient le point C.
- 2.
Trace l'hypoténuse AC.
- 3.
Tracer un arc de cercle centré en C, rayon r = AB/2 = CB, qui coupe l'hypoténuse en D.
- 4.
Tracer un arc de cercle centré en A, rayon r = AD, qui coupe le segment AB en E. Le point E proportionne le segment AB selon le nombre d'or.
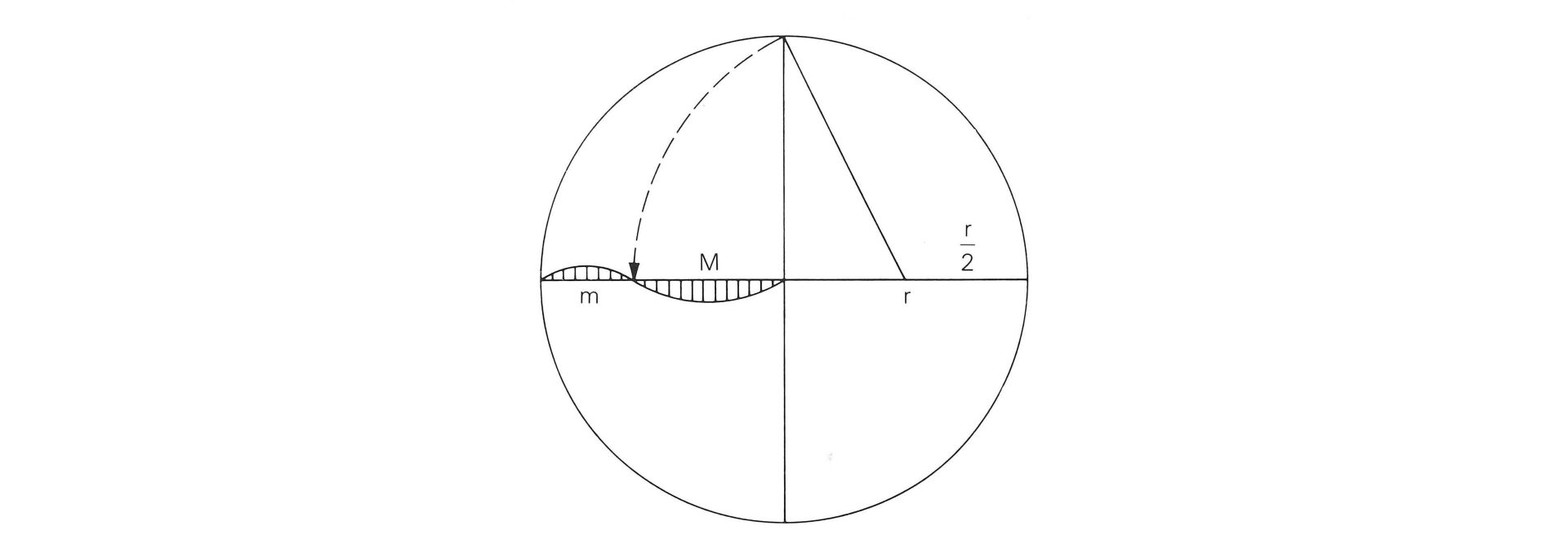
Construction du nombre d'or sur le rayon d'un cercle donné:
Calcul algébrique
Dans l'équation générale de la proportion constante, nous prenons:
x2 ± mx = m2
m = 1
Le nombre proportionnel du nombre d'or s'obtient comme suit:
x2 + x = 1
x = –½ + √¼ + 1
x = –½ (1 – √5)
soit: x = 0,61803....
Caractéristiques de la fraction:
1/0,61803... = 1,61803...
La division 1:0,61803... correspond à l'agrandissement du nombre d'or.
Exemples de nombres proportionnels du «nombre d'or»:
Documentation
Représentation graphique des principales proportions de la façade frontale du Parthénon
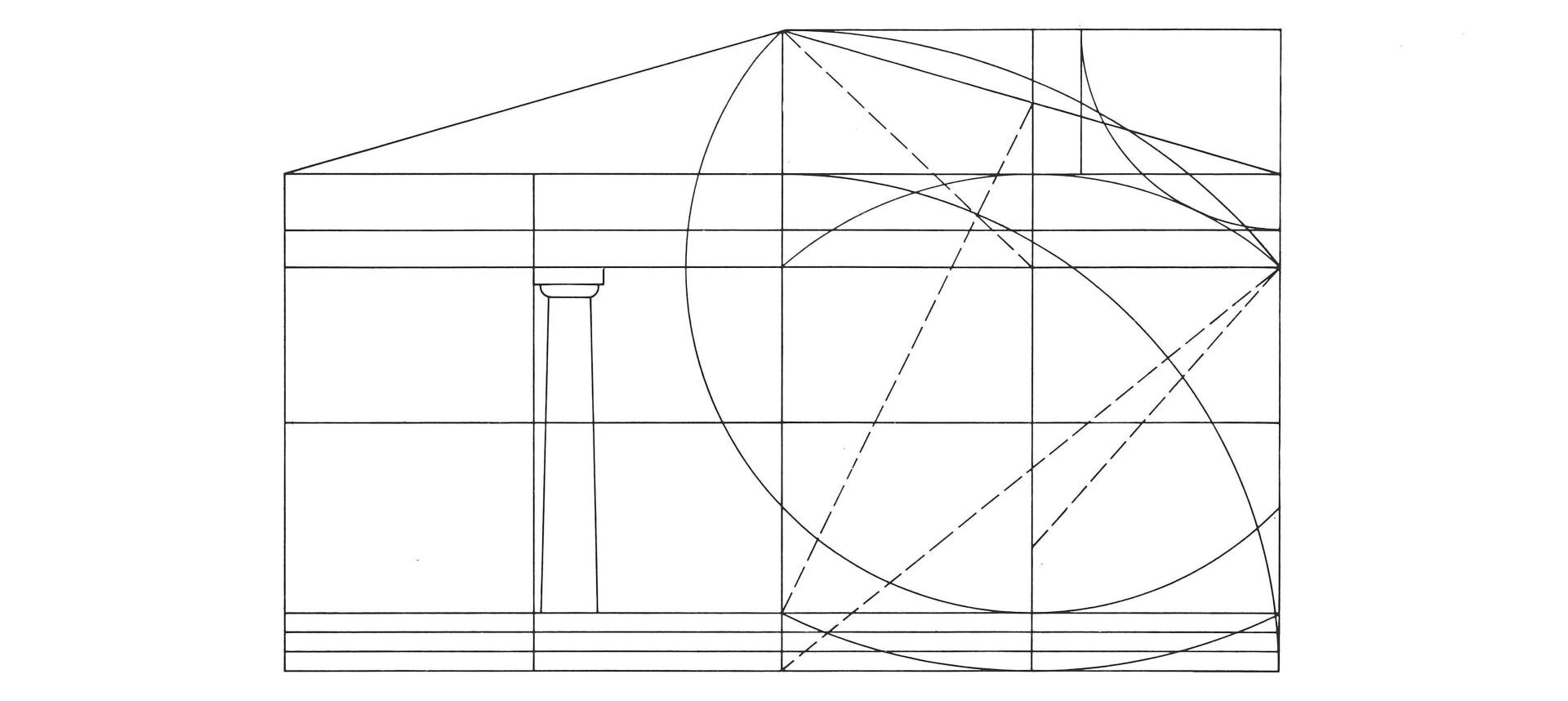
Façade frontale du Parthénon
Principe du «compas d'or» servant à la construction de segments proportionnés selon le nombre d'or
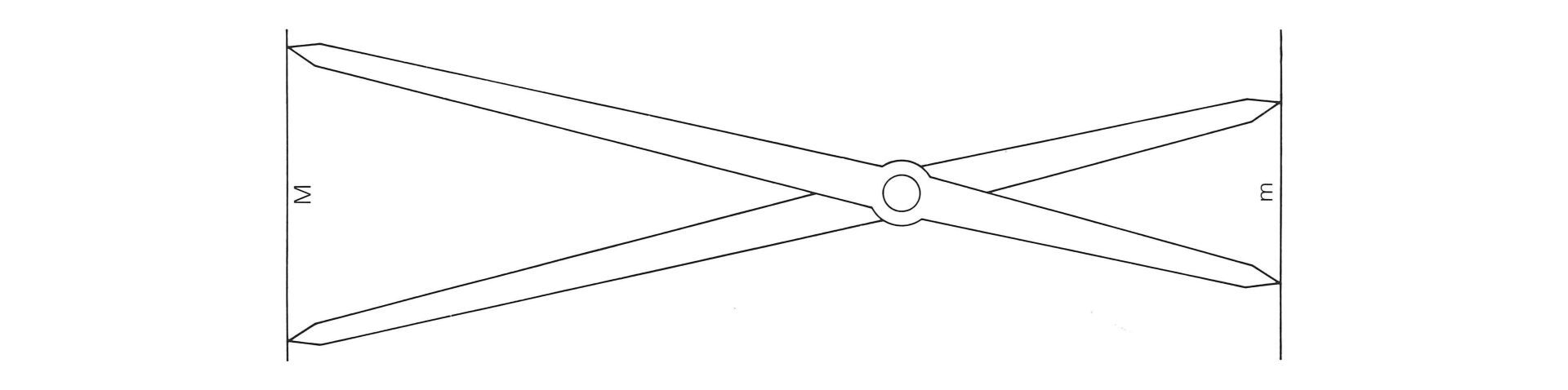
Compas d'or
Représentations schématiques d'éléments naturels où l'on retrouve les proportions exactes du nombre d'or
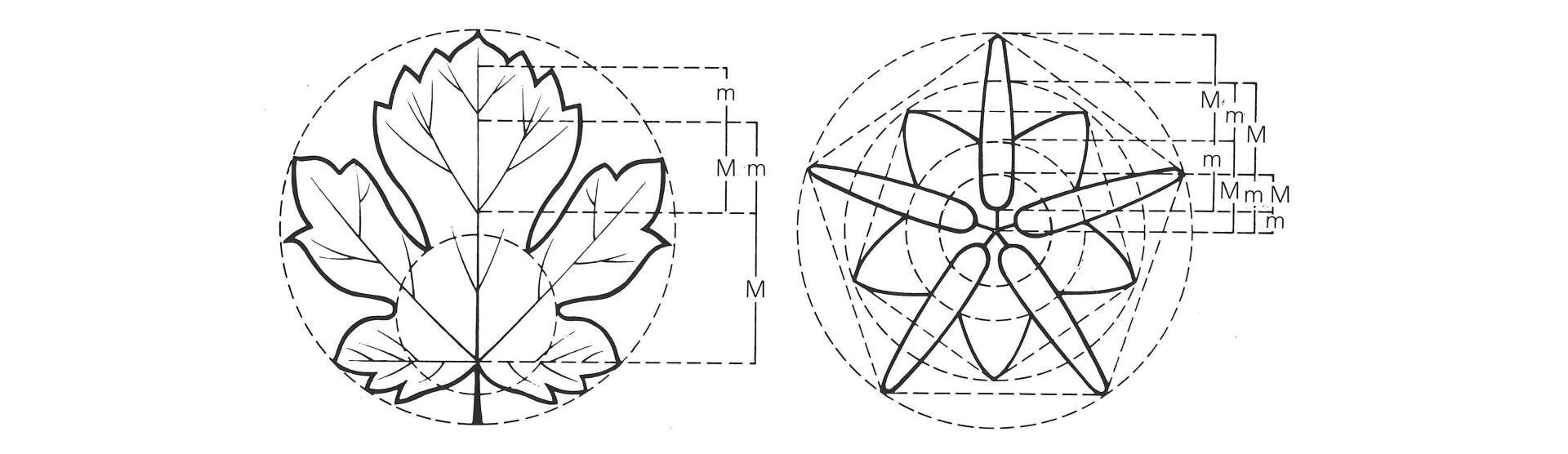
Eléments naturels avec des proportions du nombre d'or
Renvoi aux sources
Renvoi aux sources des illustrations et aux documents utilisés:
– Bruno Munari, «Discovery of the Square»
– Otto Hagenmeier, «Der Goldene Schnitt», Ernst-Moos-Verlag, Heidelberg 1963
– Ernst Neufert, «Bauordnungslehre», Bauverlag GmbH. Wiesbaden-Berlin 1965